В мире информатики и математики

1. 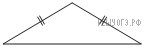Бо­ко­вая сто­ро­на рав­но­бед­рен­но­го тре­уголь­ни­ка равна 34, а ос­но­ва­ние равно 60. Най­ди­те пло­щадь этого тре­уголь­ни­ка.

2.

Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, изоб­ражённого на ри­сун­ке.

3. На сто­ро­не BC пря­мо­уголь­ни­ка ABCD, у ко­то­ро­го AB = 24 и AD = 31, от­ме­че­на точка E так, что ∠EAB = 45°. Най­ди­те ED.

4. Вы­со­та BH па­рал­ле­ло­грам­ма ABCD делит его сто­ро­ну AD на от­рез­ки AH=1 и HD=63. Диа­го­наль па­рал­ле­ло­грам­ма BD равна 65. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма.

5. Диа­го­наль AC па­рал­ле­ло­грам­ма ABCD об­ра­зу­ет с его сто­ро­на­ми углы, рав­ные 30° и 45° . Най­ди­те боль­ший угол па­рал­ле­ло­грам­ма. Ответ дайте в гра­ду­сах.

6. Сто­ро­на тре­уголь­ни­ка равна 18, а вы­со­та, про­ведённая к этой сто­ро­не, равна 17. Най­ди­те пло­щадь этого тре­уголь­ни­ка.

7. В рав­но­бед­рен­ном тре­уголь­ни­ке . Най­ди­те , если вы­со­та .

8. Най­ди­те пло­щадь пря­мо­уголь­ни­ка, если его пе­ри­метр равен 44 и одна сто­ро­на на 2 боль­ше дру­гой.

9. Ос­но­ва­ния тра­пе­ции равны 18 и 12, одна из бо­ко­вых сто­рон равна 6, а синус угла между ней и одним из ос­но­ва­ний равен . Най­ди­те пло­щадь тра­пе­ции.

10. Вы­со­та BH ромба ABCD делит его сто­ро­ну AD на от­рез­ки AH = 24 иHD = 2. Най­ди­те пло­щадь ромба.

11. Вы­со­та рав­но­бед­рен­ной тра­пе­ции, про­ведённая из вер­ши­ны C, делит ос­но­ва­ние AD на от­рез­ки дли­ной 1 и 5. Най­ди­те длину ос­но­ва­ния BC.

12. В тре­уголь­ни­ке одна из сто­рон равна 10, дру­гая равна , а угол между ними равен 120°. Най­ди­те пло­щадь тре­уголь­ни­ка.

13. Два ка­те­та пря­мо­уголь­но­го тре­уголь­ни­ка равны 4 и 10. Най­ди­те пло­щадь этого тре­уголь­ни­ка.

14. Ос­но­ва­ния тра­пе­ции равны 5 и 40, одна из бо­ко­вых сто­рон равна 14, а ко­си­нус угла между ней и одним из ос­но­ва­ний равен . Най­ди­те пло­щадь тра­пе­ции.

15. Пло­щадь па­рал­ле­ло­грам­ма ABCD равна 124. Точка E — се­ре­ди­на сто­ро­ны AB. Най­ди­те пло­щадь тра­пе­ции EBCD.

16. В тре­уголь­ни­ке одна из сто­рон равна 10, дру­гая равна 12, а угол между ними равен 30°. Най­ди­те пло­щадь тре­уголь­ни­ка.

17. Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 15 и 25, а её бо­ко­вые сто­ро­ны равны 13. Най­ди­те пло­щадь тра­пе­ции.

18. Пе­ри­метр рав­но­сто­рон­не­го тре­уголь­ни­ка равен 30. Най­ди­те его пло­щадь, делённую на .

19. Ос­но­ва­ния тра­пе­ции равны 18 и 10, одна из бо­ко­вых сто­рон равна , а угол между ней и одним из ос­но­ва­ний равен 120°. Най­ди­те пло­щадь тра­пе­ции.

20. В тра­пе­ции ABCD из­вест­но, что AD=6, BC=5, а её пло­щадь равна 22. Най­ди­те пло­щадь тре­уголь­ни­ка ABC.

21. В тре­уголь­ни­ке  из­вест­но, что  - сред­няя линия. Пло­щадь тре­уголь­ни­ка  равна 38. Най­ди­те пло­щадь тре­уголь­ни­ка .

22. Най­ди­те пло­щадь пря­мо­уголь­ни­ка, если его пе­ри­метр равен 102, а от­но­ше­ние со­сед­них сто­рон равно 2:15.

23. В пря­мо­уголь­ном тре­уголь­ни­ке один из ка­те­тов равен , угол, ле­жа­щий на­про­тив него, равен 60°, а ги­по­те­ну­за равна 20. Най­ди­те пло­щадь тре­уголь­ни­ка, делённую на .

24. В тре­уголь­ни­ке ABC от­ре­зок DE — сред­няя линия. Пло­щадь тре­уголь­ни­ка CDE равна 97. Най­ди­те пло­щадь тре­уголь­ни­ка ABC.

25. Най­ди­те пло­щадь пря­мо­уголь­ни­ка, если его пе­ри­метр равен 60, а от­но­ше­ние со­сед­них сто­рон равно 4:11.

26. Ра­ди­ус круга равен 1. Най­ди­те его пло­щадь, де­лен­ную на π.

27. Сред­няя линия тра­пе­ции равна 11, а мень­ше ос­но­ва­ние равно 5. Най­ди­те боль­шее ос­но­ва­ние тра­пе­ции.

28. Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 4 и 14, бо­ко­вая сто­ро­на равна 13. Най­ди­те длину диа­го­на­ли тра­пе­ции.

29. В тре­уголь­ни­ке одна из сто­рон равна 10, а опу­щен­ная на нее вы­со­та — 5. Най­ди­те пло­щадь тре­уголь­ни­ка.

30. Пе­ри­метр рав­но­бед­рен­но­го тре­уголь­ни­ка равен 216, а бо­ко­вая сто­ро­на — 78. Най­ди­те пло­щадь тре­уголь­ни­ка.

31. Вы­со­та рав­но­сто­рон­не­го тре­уголь­ни­ка равна 10. Най­ди­те его пло­щадь, делённую на 

32. В тре­уголь­ни­ке ABC из­вест­но, что DE — сред­няя линия. Пло­щадь тре­уголь­ни­ка CDE равна 24. Най­ди­те пло­щадь тре­уголь­ни­ка ABC.

33. Одна из сто­рон па­рал­ле­ло­грам­ма равна 12, а опу­щен­ная на нее вы­со­та равна 10. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма.

34. Най­ди­те пло­щадь кру­го­во­го сек­то­ра, если длина огра­ни­чи­ва­ю­щей его дуги равна 6π, угол сек­то­ра равен 120°, а ра­ди­ус круга равен 9. В ответ ука­жи­те число, де­лен­ную на π.

35. Вы­со­та  ромба  делит его сто­ро­ну  на от­рез­ки  и . Най­ди­те пло­щадь ромба.

36. Пе­ри­метр ромба равен 24, а тан­генс од­но­го из углов равен . Най­ди­те пло­щадь ромба.

37. В ромбе сто­ро­на равна 10, одна из диа­го­на­лей — 10, а угол, ле­жа­щий на­про­тив этой диа­го­на­ли, равен 60°. Най­ди­те пло­щадь ромба, де­лен­ную на 

38. Сто­ро­на тре­уголь­ни­ка равна 18, а вы­со­та, про­ведённая к этой сто­ро­не, равна 22. Най­ди­те пло­щадь этого тре­уголь­ни­ка.

39. Бо­ко­вая сто­ро­на тра­пе­ции равна 5, а один из при­ле­га­ю­щих к ней углов равен 30°. Най­ди­те пло­щадь тра­пе­ции, если её ос­но­ва­ния равны 3 и 9.

40. В тра­пе­ции ABCD из­вест­но, что AD = 8, BC = 5, а её пло­щадь равна 52. Най­ди­те пло­щадь тра­пе­ции BCNM, где MN – сред­няя линия тра­пе­ции ABCD.

41. Одна из сто­рон па­рал­ле­ло­грам­ма равна 12, дру­гая равна 5, а ко­си­нус од­но­го из углов равен . Най­ди­те пло­щадь па­рал­ле­ло­грам­ма.

42. Ос­но­ва­ния тра­пе­ции равны 7 и 63, одна из бо­ко­вых сто­рон равна 18, а ко­си­нус угла между ней и одним из ос­но­ва­ний равен . Най­ди­те пло­щадь тра­пе­ции.

43. В тре­уголь­ни­ке ABC от­ме­че­ны се­ре­ди­ны M и N сто­рон BC и AC со­от­вет­ствен­но. Пло­щадь тре­уголь­ни­ка CNM равна 89. Най­ди­те пло­щадь четырёхуголь­ни­ка ABMN.

44. Вы­со­та  ромба  делит его сто­ро­ну  на от­рез­ки  и . Най­ди­те пло­щадь ромба.

45. Вы­со­та  ромба  делит его сто­ро­ну  на от­рез­ки  и . Най­ди­те пло­щадь ромба.

46. В пря­мо­уголь­ни­ке одна сто­ро­на равна 10, дру­гая сто­ро­на равна 12. Най­ди­те пло­щадь пря­мо­уголь­ни­ка.За­да­ние 11 № 169864

47. В тра­пе­ции ABCD из­вест­но, что AD=4, BC=1, а её пло­щадь равна 35. Най­ди­те пло­щадь тре­уголь­ни­ка ABC.

48. Из квад­ра­та вы­ре­за­ли пря­мо­уголь­ник (см. ри­су­нок). Най­ди­те пло­щадь по­лу­чив­шей­ся фи­гу­ры.

49. В пря­мо­уголь­ном тре­уголь­ни­ке один из ка­те­тов равен 35, а угол, ле­жа­щий на­про­тив него равен 45∘. Най­ди­те пло­щадь тре­уголь­ни­ка.

50. В тра­пе­ции ABCD из­вест­но, что AD = 5, BC = 1, а её пло­щадь равна 12. Най­ди­те пло­щадь тра­пе­ции BCNM, где MN – сред­няя линия тра­пе­ции ABCD.