Подготовка к переводному экзамену_10 класс

1. В окружности с центром  отрезки  и  - диаметры. Центральный угол  равен 138°. Найдите вписанный угол . Ответ дайте в градусах.

2. Точка О — центр окруж­но­сти, ∠ACB = 24° (см. ри­су­нок). Най­ди­те ве­ли­чи­ну угла AOB (в гра­ду­сах).

3. Четырехугольник ABCD впи­сан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Най­ди­те угол ABD. Ответ дайте в градусах.

4. Ра­ди­ус окруж­но­сти с цен­тром в точке O равен 85, длина хорды AB равна 102 (см. рисунок). Най­ди­те рас­сто­я­ние от хорды AB до па­рал­лель­ной ей ка­са­тель­ной k.

5. Из точки А про­ве­де­ны две ка­са­тель­ные к окруж­но­сти с цен­тром в точке О. Най­ди­те ра­ди­ус окружности, если угол между ка­са­тель­ны­ми равен 60°, а рас­сто­я­ние от точки А до точки О равно 8.

6. Прямая ка­са­ет­ся окруж­но­сти в точке K. Точка O — центр окружности. Хорда KM об­ра­зу­ет с ка­са­тель­ной угол, рав­ный 40°. Най­ди­те ве­ли­чи­ну угла KOM. Ответ дайте в градусах.

7. 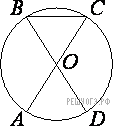AC и BD — диа­мет­ры окруж­но­сти с цен­тром O. Угол ACB равен 12°. Най­ди­те угол AOD. Ответ дайте в градусах.

8. На отрезке  выбрана точка  так, что  и . Построена окружность с центром , проходящая через . Найдите длину отрезка касательной, проведённой из точки  к этой окружности.

9. Центр окружности, описанной около треугольника , лежит на стороне . Радиус окружности равен 8,5. Найдите , если .

10. AC и BD — диа­мет­ры окруж­но­сти с цен­тром O. Угол ACB равен 18°. Най­ди­те угол AOD. Ответ дайте в градусах.

Подготовка к экзамену_

1. Найдите значение выражения 

2. Найдите зна­че­ние вы­ра­же­ния 

3. В вы­бо­рах участ­во­ва­ли два кандидата. Го­ло­са из­би­ра­те­лей рас­пре­де­ли­лись между ними в от­но­ше­нии 3:2. Сколь­ко про­цен­тов го­ло­сов по­лу­чил проигравший?

4. Длина ме­ди­а­ны , проведённой к сто­ро­не тре­уголь­ни­ка со сто­ро­на­ми ,  и , вы­чис­ля­ет­ся по фор­му­ле . Тре­уголь­ник имеет сто­ро­ны 5, 9 и 10. Най­ди­те длину медианы, проведённой к сто­ро­не длины 9.

5. Найдите значение выражения 

6.

В квартире, где проживает Алексей, установлен прибор учёта расхода горячей воды (счётчик). 1 марта счётчик показывал расход 838 куб.м воды, а 1 апреля — 845 куб.м. Какую сумму должен заплатить Алексей за горячую воду за март, если цена 1 куб.м горячей воды составляет 79 руб.? Ответ дайте в рублях.

7. Найдите ко­рень урав­не­ния .

8. Какой наи­мень­ший угол в гра­ду­сах об­ра­зу­ют ми­нут­ная и ча­со­вая стрел­ки в семь часов утра?

9. Установите со­от­вет­ствие между ве­ли­чи­на­ми и их воз­мож­ны­ми значениями: к каж­до­му элементу пер­во­го столбца под­бе­ри­те соответствующий эле­мент из вто­ро­го столбца.

ВЕЛИЧИНЫ		ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
А) ра­ди­ус Земли Б) рост жирафа В) ши­ри­на футбольного поля Г) тол­щи­на лезвия бритвы		1) 68 м 2) 500 см 3) 0,08 мм 4) 6400 км

Запишите в ответ цифры, рас­по­ло­жив их в порядке, со­от­вет­ству­ю­щем буквам:

A	Б	В	Г

10. В груп­пе ту­ри­стов 30 человек. Их за­бра­сы­ва­ют в труд­но­до­ступ­ный район вертолётом в не­сколь­ко приёмов по 3 че­ло­ве­ка за рейс. Порядок, в ко­то­ром вертолёт пе­ре­во­зит туристов, случаен. Най­ди­те ве­ро­ят­ность того, что ту­рист Н. по­ле­тит четвёртым рей­сом вертолёта.

11. На диаграмме показана среднемесячная температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев, когда среднемесячная температура была отрицательной.

12. Телефонная компания предоставляет на выбор три тарифных плана.

Тарифный план	Абонентская плата (в месяц)	Плата за 1 минуту разговора
«Повременный»	Нет	0,4 руб.
«Комбинированный»	180 руб. за 400 мин.	0,3 руб. (сверх 400 мин. в месяц)
«Безлимитный»	245	Нет

Абонент предполагает, что общая длительность разговоров составит 500 минут в месяц, и исходя из этого выбирает наиболее дешёвый тарифный план. Сколько рублей должен будет заплатить абонент за месяц, если общая длительность разговоров действительно будет равна 500 минутам?

13. Найдите объем многогранника, изоб­ра­жен­но­го на ри­сун­ке (все дву­гран­ные углы прямые).

14. Задание 14.1.

На ри­сун­ке изображён гра­фик функ­ции y = f(x) и от­ме­че­ны точки A, B, C и D на оси x. Поль­зу­ясь графиком, по­ставь­те в со­от­вет­ствие каж­дой точке ха­рак­те­ри­сти­ку функ­ции и её производной.

Ниже ука­за­ны зна­че­ния про­из­вод­ной в дан­ных точках. Поль­зу­ясь графиком, по­ставь­те в со­от­вет­ствие каж­дой точке зна­че­ние про­из­вод­ной в ней.

ТОЧКИ		ХАРАКТЕРИСТИКИ ФУНК­ЦИИ ИЛИ ПРОИЗВОДНОЙ
А) A Б) B В) C Г) D		1) Про­из­вод­ная отрицательна, функ­ция положительна. 2) Про­из­вод­ная положительна, функ­ция отрицательна. 3) Функ­ция отрицательна, про­из­вод­ная отрицательна. 4) Функ­ция положительна, про­из­вод­ная равна 0.

В таб­ли­це под каж­дой бук­вой ука­жи­те со­от­вет­ству­ю­щий номер.

А	Б	В	Г

Задание 14.2.

На ри­сун­ке изоб­ра­же­на срав­ни­тель­ная диа­грам­ма еже­ме­сяч­ных объёмов про­даж те­ле­ви­зо­ров марок Samsung и Philips в 2012 году в ма­га­зи­не радиоэлектроники. По го­ри­зон­та­ли ука­зы­ва­ют­ся месяцы, по вер­ти­ка­ли — ко­ли­че­ство про­дан­ных телевизоров.

Пользуясь диаграммой, по­ставь­те в со­от­вет­ствие каж­до­му из ука­зан­ных пе­ри­о­дов вре­ме­ни ха­рак­те­ри­сти­ку про­даж в этот период.

ПЕРИОДЫ ВРЕМЕНИ		ХАРАКТЕРИСТИКИ ДАВЛЕНИЯ
А) 1-й квар­тал года Б) 2-й квар­тал года В) 3-й квар­тал года Г) 4-й квар­тал года		1) Про­да­жи те­ле­ви­зо­ров марки Philips росли. 2) Про­да­жи те­ле­ви­зо­ров марки Samsung падали. 3) Про­да­но боль­ше всего те­ле­ви­зо­ров марки Samsung по срав­не­нию с осталь­ны­ми квар­та­ла­ми года. 4) Те­ле­ви­зо­ров марки Philips про­да­но около 450 штук.

В таб­ли­це под каж­дой бук­вой ука­жи­те со­от­вет­ству­ю­щий номер.

А	Б	В	Г

Выберите любое из предложенных заданий и решите его.

15. Найдите ординату точки пересечения прямой, заданной уравнением 3x + 2y = 6, с осью Oy.

16. Пло­щадь ос­но­ва­ния ко­ну­са равна 18. Плос­кость, па­рал­лель­ная плос­ко­сти ос­но­ва­ния ко­ну­са, делит его вы­со­ту на от­рез­ки дли­ной 3 и 6, счи­тая от вер­ши­ны. Най­ди­те пло­щадь се­че­ния ко­ну­са этой плос­ко­стью.

17. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.

НЕРАВЕНСТВА		РЕШЕНИЯ
А)  Б)  В)  Г)		1)  2)  3)  4)

Впишите в приведённую в ответе таблицу под каждой буквой соответствующий решению номер.

18. Двадцать вы­пуск­ни­ков од­но­го из один­на­дца­тых клас­сов сда­ва­ли ЕГЭ по обществознанию. Самый низ­кий по­лу­чен­ный балл был равен 36, а самый вы­со­кий — 75. Вы­бе­ри­те утверждения, ко­то­рые верны при ука­зан­ных условиях.

1) Среди этих вы­пуск­ни­ков есть человек, ко­то­рый по­лу­чил 75 бал­лов за ЕГЭ по обществознанию.

2) Среди этих вы­пуск­ни­ков есть два­дцать два че­ло­ве­ка с рав­ны­ми бал­ла­ми за ЕГЭ по обществознанию.

3) Среди этих вы­пуск­ни­ков есть человек, по­лу­чив­ший 20 бал­лов за ЕГЭ по обществознанию.

4) Баллы за ЕГЭ по об­ще­ст­во­зна­нию лю­бо­го из этих два­дца­ти че­ло­век не ниже 35.

В от­ве­те за­пи­ши­те но­ме­ра вы­бран­ных утвер­жде­ний без пробелов, за­пя­тых и дру­гих до­пол­ни­тель­ных символов.

19. Вычеркните в числе 141565041 три цифры так, чтобы по­лу­чив­ше­е­ся число де­ли­лось на 30. В от­ве­те ука­жи­те ровно одно по­лу­чив­ше­е­ся число.

20. В ма­га­зи­не бы­то­вой тех­ни­ки объём про­даж хо­ло­диль­ни­ков носит се­зон­ный характер. В ян­ва­ре было про­да­но 10 холодильников, и в три по­сле­ду­ю­щих ме­ся­ца про­да­ва­ли по 10 холодильников. С мая про­да­жи уве­ли­чи­ва­лись на 15 еди­ниц по срав­не­нию с преды­ду­щим месяцем. С сен­тяб­ря объём про­даж начал умень­шать­ся на 15 хо­ло­диль­ни­ков каж­дый месяц от­но­си­тель­но преды­ду­ще­го месяца. Сколь­ко хо­ло­диль­ни­ков про­дал ма­га­зин за год?